Interferometry

Ice thickness is determined by in-situ laser measurment (e.g. HeNe laser with a fixed wavelength of λ0 = 632.8 nm). The laser beam is positioned so that it reflects off the centre of the substrate and the reflected beam is measured with a photodiode

Note

• Include diagram of the setup
  • position of the laser
  • position of the detector

As monochromatic light is shone onto an ice film, the light can be reflected from the vacuum-ice interface or the ice-substrate interface. The reflected light sin-waves interacts and interference patterns appears due to the constructive and destructive interference arising from the increasing ice thickness as shown in Fig. 1.

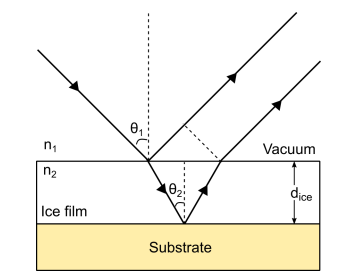
Fig. 1 Taken from Rachael, to redo

Note

• add svg sin wave to show constructive, destructive interference

Warning

Rachael uses the half period (remove the 2 in the equation), why?

\[y = y_0 + A sin(\frac{2\pi}{w}(x-x_c))\]

where \(y_0\) is the vertical offset, \(A\) is the amplitude, \(x_c\) is the horizontal offset and \(w\) is the period (i.e. \(2\pi/w\) is the frequency).

We define the sine function ‘sinfit(x, *p)’ for the fit with some initial guesses, which can be edited accordingly.

• A is obtained from the fit

Ice Refractive index

Theory

• Symbol: n

It is used to describe the optical properties of a pure medium and is a complex function of two parameters:

• k imaginary index - describe the attenuation or the absorbtion of the medium
• n real refractive index - it is the ratio of the velocity of light within the mediumwith respect to the speed of light in vacuum

Both k and n are wavelength dependant, hence require investigation over the whole electromagnetic spectrum:

• []: UV investigation (Amorphous and crystaline water ice)

Warning

• How does ice porosity affect the refractive index
• How has he been determined in the IR range.
  • Should I use value of the litterature rather than the laser diode signal ?

Then we can estimate the refractive index of the ice (n₂), can be estimated using the following equation

\[n_2 = \frac{y_0 + A}{y_0 - A}\]

Using Snell’s Laaw (\(n_1 sinθ_1 = n_2 sinθ_2\))

\[θ_2 = sin^{-1} (\frac{n_1 sinθ_1}{n_2})\]

\[d_{fringe} = \frac{λ_0}{n_2 cosθ_2}\]

Warning

Difference in fitting from different molecules

• single vs binary mixtures

To see how this is translated into code visit the folloing page []